Researchers at Alibaba Cloud Computing have released new work showing that large language models (LLMs) can be trained more efficiently when the learning curriculum is adjusted on the fly using statistical signals collected during reinforcement learning.
The study, carried out by Guochao Jiang and colleagues, introduces “Variance-based Curriculum Reinforcement Learning” (VCRL). Tested on two open Qwen3 base models—Qwen3-4B-Base and Qwen3-8B-Base—VCRL delivered the best-to-date scores on five well-known mathematics benchmarks, surpassing existing reinforcement-learning techniques such as Group Relative Policy Optimization (GRPO), DAPO, and GSPO. In the larger 8-billion-parameter model, the new method lifted the average benchmark score from 32.96 (untrained base) to 57.76, outstripping the strongest previous baseline by more than four points.
What’s New?
The core novelty lies in treating the reinforcement-learning training set as a dynamic curriculum whose difficulty is estimated directly from the model’s own rollouts. Instead of feeding the model a random assortment of math problems, VCRL screens each sample by measuring the variance of the rewards obtained across several generated solutions for that same prompt.
- Low variance means the problem is either too easy (the model almost always gets it right) or too hard (it nearly always fails).
- High variance indicates the model is in a productive learning zone—it sometimes succeeds and sometimes fails—so gradients computed from that sample are more informative.
By keeping high-variance (“moderately difficult”) samples in the training batch and stashing them for replay, VCRL accelerates skill acquisition without wasting compute on examples the model has already mastered or those it cannot solve yet. The approach is fully automatic; no manual labeling of difficulty or extra reward engineering is required.
How It Works?
The study builds on the rollout-based reinforcement-learning framework popularized by GRPO. In GRPO, the language model—acting as a policy—generates multiple candidate answers (a “group”) for a given math question. A verifier awards a binary reward (1 for a correct answer, 0 otherwise). Relative advantages are computed inside the group, allowing the policy to move probability mass toward trajectories that scored higher.
VCRL adds two mechanisms on top of this recipe:
- Variance-based Dynamic Sampling. For each question, the team looks at the distribution of rewards across G generated attempts. Mathematically, if k of the G attempts are correct, the unbiased variance estimator is k(G-k)/[G(G-1)]. That value is normalized to lie between 0 and 1. Only questions whose normalized variance p exceeds a threshold κ are kept in the active training batch.
- Replay Learning with a Memory Bank. Questions that pass the variance filter are stored in a priority queue. During subsequent mini-batches, if too many incoming questions are filtered out, the algorithm replenishes the batch by replaying cached high-variance items. Priorities are updated with an exponential-moving-average rule so that heavily replayed items eventually age out.
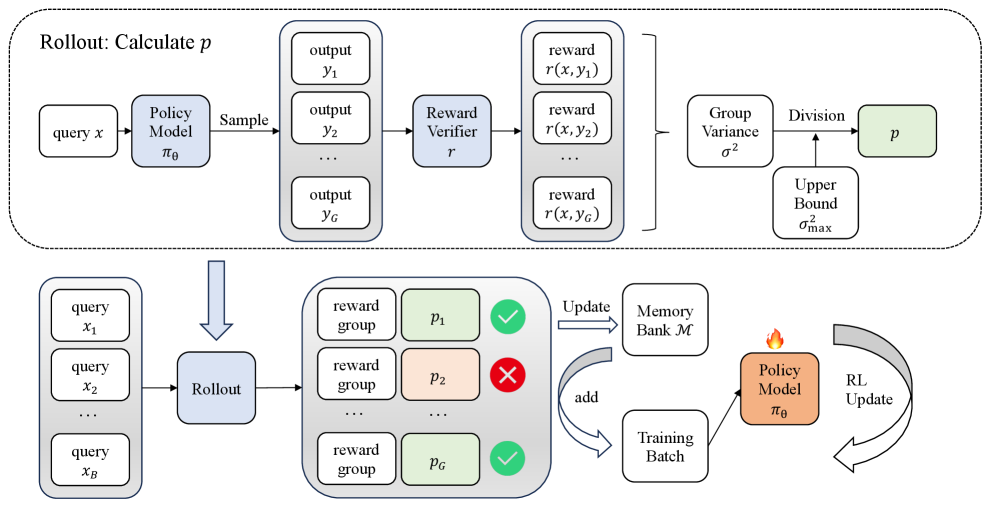
This curriculum is self-correcting. At early training steps, many questions look hard; variance is high, so the filter admits plenty of examples. As the model improves, those same questions become easy; their variance drops and they automatically fall out of the curriculum, making room for new challenges.
Technical Details
The experiments use the public Qwen3 base checkpoints released earlier this year:
- Qwen3-4B-Base (4.1 billion parameters)
- Qwen3-8B-Base (7.9 billion parameters)
Both models were further trained for 500 reinforcement-learning steps on the 17-k-prompt DAPO-Math-17K dataset. Each prompt was expanded into G = 16 rollouts with a maximum length of 4,096 tokens. The verifier provides a sparse 0/1 reward by checking the final numeric answer.
Key hyper-parameters:
- Batch size = 128 prompts
- Optimizer: AdamW with a fixed learning rate of
1 × 10-6
- Early steps use a permissive variance threshold (κ = 0.3) to seed the replay bank; after 20 steps it tightens to κ = 0.8 for sharper focus
- Momentum constant for priority updates α = 0.9
- Each cached problem can be replayed at most twice to maintain diversity
The researchers evaluated every 20 steps on five public mathematics benchmarks that stress different reasoning regimes:
- AIME-2024 (American Invitational Math Exam)
- AIME-2025
- MATH500 (a curated 500-problem subset from the MATH dataset)
- OlympiadBench (mixed national Olympiad problems)
- AMC23 (American Mathematics Contest 10/12 years 2000-2023)
Following recent best practice, each test set problem was sampled 16 times at inference with temperature 0.6 and top-p 0.95; accuracy is reported as avg@16.
Performance Snapshot (Qwen3-8B-Base)
| Training method |
AIME-24 |
AIME-25 |
MATH500 |
OlympiadBench |
AMC23 |
Average |
| Base model |
10.83 |
10.00 |
68.75 |
34.10 |
41.11 |
32.96 |
| GRPO |
23.13 |
21.88 |
86.94 |
54.02 |
65.29 |
50.25 |
| DAPO |
22.08 |
20.42 |
87.14 |
53.52 |
64.01 |
49.43 |
| GSPO |
27.29 |
22.92 |
89.23 |
56.75 |
69.28 |
53.09 |
| VCRL (new) |
34.38 |
27.08 |
91.99 |
60.21 |
75.15 |
57.76 |
The margins are most striking on the toughest datasets. VCRL nearly triples AIME-2024 accuracy versus the base model and stays six to seven points ahead of GSPO. On the moderately difficult MATH500, gains are smaller because all methods already exceed 85 percent, but VCRL still edges forward.
Component Ablations
To understand where the improvements come from, the team performed stepwise ablations starting with vanilla GRPO:
| Model |
Average score across five benchmarks |
| Qwen3-4B-Base (no RL) |
26.68 |
| + GRPO |
41.76 |
| + Variance-based Dynamic Sampling |
44.73 |
| + Replay Learning (full VCRL) |
49.43 |
Each added piece provides a clear incremental benefit. Replay learning, in particular, yields the largest extra jump, indicating that revisiting informative problems reinforces newly acquired skills.
Summary
Alibaba Cloud’s VCRL demonstrates that how we pick training examples during reinforcement learning can matter as much as the optimizer itself. By quantifying problem difficulty directly from reward variance, the method constructs an implicit “just-right” curriculum that evolves with the model. The results on both the 4-billion and 8-billion Qwen3 bases show substantial headroom still exists in mid-sized open models when smarter data-selection strategies are used.
While the study focuses on mathematics, the underlying idea—using rollout variance as a proxy for learning potential—could apply to code generation, scientific reasoning, or any domain with sparse verifiable rewards. The authors note that VCRL is implementation-agnostic: it can layer on top of GRPO, GSPO, or future rollout-based variants with minimal code changes.
Next steps include scaling to larger models, testing under noisy reward conditions, and integrating domain-specific difficulty heuristics. For now, VCRL offers a promising, lightweight tool for teams looking to push open-weight LLMs closer to competition-grade mathematical reasoning.